App installieren
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Anmerkung: This feature may not be available in some browsers.
Interner Zinsfuß bei 3 jähriger Laufzeit
- Ersteller DerSinger
- Erstellt am
Hier sitze ich auch gerade dran.
Wo steht denn dieser Lösungsansatz von Monique im Skript?
In der Kurseinheit 2 ab Seite 38.
Du musst schauen welcher der 4 Sonderfälle gegeben ist, wenn du einen Zinsfiuß berechnen sollst.
Hatte hier gerade einen aha moment. Danke ab Monique79!
Hierzu noch eine frage.Sehe ich das richtig, dass der interne Zinsfuß sich für Auswahlentscheidungen zwischen Projekten nicht eignet?
Hierzu noch eine frage.Sehe ich das richtig, dass der interne Zinsfuß sich für Auswahlentscheidungen zwischen Projekten nicht eignet?
Sehe ich das richtig, dass der interne Zinsfuß sich für Auswahlentscheidungen zwischen Projekten nicht eignet?
Ja genau, er sagt nichts über die vorteilhaftigkeit von Projekten aus.
Aber der Interne Zinsfuß sagt was über die Vorteilhaftigkeit über ein Projekt aus!
Eine Investition ist genau dann vorteilhaft, wenn r >= i d.h. wenn der interne Zinfuß nicht kleiner als der Kalkulationszins ist!
Eine Investition ist genau dann vorteilhaft, wenn r >= i d.h. wenn der interne Zinfuß nicht kleiner als der Kalkulationszins ist!
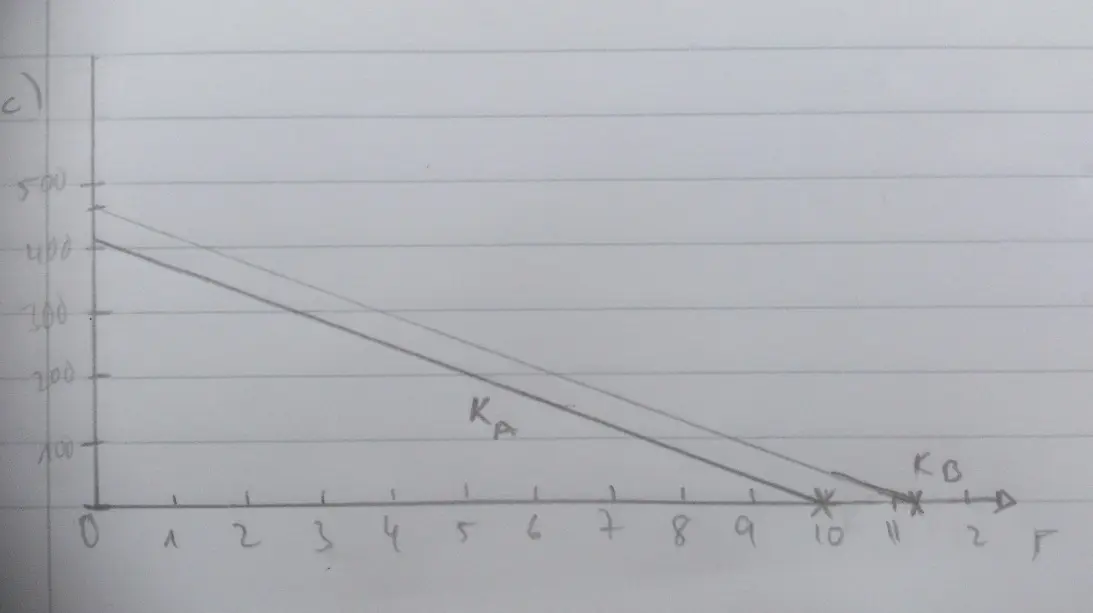
an Zoffchen, bei der Skize der Kapitalwertfunktionen gehen bei mir beide Kaitalwertfunktionen zu r = 10,25. Bei CA=456 und bei CB=405. Wie kommst du auf auf r =10 und r=11,2?Sieht bei noch jemandem die Skizze zur Kapitalwertfunktion so aus?
ich habe einmal eine sau blöde Frage 😱
Aber wie kommt man bei der Skizze denn auf die Werte der y-Achse?
Stehe gerade übelst auf dem Schlauch diesbezüglich....
Sind das die Kapitalwerte aus Aufgabenteil a? Falls ja, bin ich völlig verwirrt... ich hab nämlich als Kapitalwert für Projekt A von 208,0445 und für Projekt B von 204,2436....
Danke für eure Hilfe.
Grüße
Aber wie kommt man bei der Skizze denn auf die Werte der y-Achse?
Stehe gerade übelst auf dem Schlauch diesbezüglich....
Sind das die Kapitalwerte aus Aufgabenteil a? Falls ja, bin ich völlig verwirrt... ich hab nämlich als Kapitalwert für Projekt A von 208,0445 und für Projekt B von 204,2436....
Danke für eure Hilfe.
Grüße
VIELEN DANK, HATTE DEN ÜBERBLICK VERLOREN!Den Zinsfuß on Projekt B haben wir doch in b) ausgerechnet: r* = 11,25
In der Beschreibung steht das der interne Zins für A = 10% ist.
Hallo,
ich habe einmal eine sau blöde Frage 😱
Aber wie kommt man bei der Skizze denn auf die Werte der y-Achse?
Stehe gerade übelst auf dem Schlauch diesbezüglich....
Sind das die Kapitalwerte aus Aufgabenteil a? Falls ja, bin ich völlig verwirrt... ich hab nämlich als Kapitalwert für Projekt A von 208,0445 und für Projekt B von 204,2436....
Danke für eure Hilfe.
Grüße
Achsenabschnitte: Für r(B)=10,25 ist K = 0. Wenn r = 0, dann beträgt Kapitalwert (B) =405
-1200 + 135*1,1125^-1 + 135*1,1125^-2 + 1335*1,1125^-3 = 0
Ja genau, er sagt nichts über die vorteilhaftigkeit von Projekten aus.
Nein, das ist so nicht richtig. Im allgemeinen eignet sich der Zinsfuß als Vorteilhaftigkeitskriterium nicht. Bei Normalinvestitionen (auf eine negative Anfangsauszahlung folgen nur positive Rücklüsse) führt der Zinsfuß auf die gleichen Vorteilhaftigkeitsaussagen, wie die anderen Kriterien.
In dieser Aufgabe gilt: Da die 5% Marktzins < als die Zinsfüsse von A und B sind, sind beide Investitionen vorteilhaft.
Sieht bei noch jemandem die Skizze zur Kapitalwertfunktion so aus?
Ich bin es schon wieder! Deine Skizze hat einen kleine Fehler:
Projekt A: K(r=0) = 456 -> zinsfuß = 10%
Projekt B: K(r=0) = 405 -> zinsfuß = 11,25%
A hat also den höheren y-Achsenabschnitt schneidet aber die x-Achse früher als B -> die Kurven müssen sich schneiden.
Schau mal nach, du hast die falschen Punkteverbunden.
Hallo,
ich habe einmal eine sau blöde Frage 😱
Aber wie kommt man bei der Skizze denn auf die Werte der y-Achse?
Stehe gerade übelst auf dem Schlauch diesbezüglich....
Sind das die Kapitalwerte aus Aufgabenteil a? Falls ja, bin ich völlig verwirrt... ich hab nämlich als Kapitalwert für Projekt A von 208,0445 und für Projekt B von 204,2436....
Danke für eure Hilfe.
Grüße
Schau mal in den Umdruck unter Zinsfuß. Beim Zeichnen einer Kapitalwertkurve sind folgende exemplarischen Punkte genannt.
1.) Schnittpunkt mit der Y-Achse: Genau dann wenn der Zinsatz Null ist
-> Kapitalwert ist die einfache Summe aller Zahlungen der
Zahlungsreihe, d.h. hier für A (-1700 + 220 +605 + 1331)= 456
2.) Schnittpunkt mit der x-Achse: Hier wird also der Kapitalwert = 0
Diesen Wert ist als Zinsfuß definiert.
3.) Geht der Zinssatz gegen unendlich, werden die die mit q hoch -T abgezinst werden Null. Der Grenzwert für Zinssatz gegen unendlich entspricht der Anfangsauszahlung (-1700 für Projekt A).
Mit diesen Angaben kann die Kurve einigermaßen skizzieren.
vielleicht könnt ihr mir noch vor der Klausur helfen. Ich erkenne zwar die 4 Sonderfälle zur Berechnung des Internen Zinsfusses die im Skript beschrieben worden sind, wüsste aber nun nicht in der Aufgabe wie ich auf 135/1200 kommen sollte. Hat jemand eventuell eine "einfache Erklärung". Monique79 meinte "der Rückfluss über die 3 ist konstant"... die Zahlungsreihe ist doch -1200, 135, 135, 1335.
Ich verstehe man muss Kapitalwert=0 setzten und nach r auflösen.
Wie würdet denn ihr:
-1200x(1+r)^-0+135x(1+r)^-1+135x(1+r)^-2+1335(1+r)^-3=0 lösen (nach r auflösen)?
Auf Lösungshinweise würde ich mich freuen.
Ich verstehe man muss Kapitalwert=0 setzten und nach r auflösen.
Wie würdet denn ihr:
-1200x(1+r)^-0+135x(1+r)^-1+135x(1+r)^-2+1335(1+r)^-3=0 lösen (nach r auflösen)?
Auf Lösungshinweise würde ich mich freuen.
Aralc, das ist der Sonderfall 4 auf S. 43 des Skripts 2 I&F (Seitenzahl stammt aus einem nicht ganz aktuellen PDF, könnte daher etwas variieren. Bei einer Auszahlung und konstanten Rückflüssen kann der interne Zinsfuß als Quotient aus e1=e2=e3 und e0 gebildet werden, daher hier im Fall: 135/1200.
Nicht gut. Kann er bitte mit seinen Mathematik- und BWLer machenJa. Das ist so eine Art Hobby von Prof. Hering. 😉
Die Sonderfälle muss man schon können - in den alten Klausuren kamen sie immer wieder vor. Wenn Du nicht lernen willst - so kompliziert sind die Sonderfälle auch nicht:
Beim Internen Zins muss man ja e0 + e1/q^1 + e2/q^2 + e3/q^3 ... = 0 setzen und dann nach q (=1+r) auflösen.
Zahlungen nur in 2 Perioden:
e0 + en/q^n = 0 --> e0 x q^n = -en --> q = n-te Wurzel aus (- en /e0)
Wenn das nun t = 0 und t = 1 ist, wird es q = - e1/e0
Für den Fall von 3 Perioden (t=0,1,2) kann man die Gleichung oben ebenfalls umstellen und mit der Mitternachtsformel dann auf die krude Wurzel-Quadrat-Gleichung kommen.
Und für e1=e2 und e3=e1+e0 rd der interne Zins durch -e1/e0 ermittelt - das kann man sich ja doch ganz gut merken. 😉 Und ist auch logisch, denn nachschüssige Zinsen in kontanter Höhe und zusätzlich in der letzten Periode die Rückzahlung der Anfangsauszahlung ist ja nix anderes, als wenn ich 1000 Euro auf ein Sparbuch lege und die 0,36 Euro, die ich dafür aktuell an Zinsen bekomme, immer am Jahresende abhebe.
Beim Internen Zins muss man ja e0 + e1/q^1 + e2/q^2 + e3/q^3 ... = 0 setzen und dann nach q (=1+r) auflösen.
Zahlungen nur in 2 Perioden:
e0 + en/q^n = 0 --> e0 x q^n = -en --> q = n-te Wurzel aus (- en /e0)
Wenn das nun t = 0 und t = 1 ist, wird es q = - e1/e0
Für den Fall von 3 Perioden (t=0,1,2) kann man die Gleichung oben ebenfalls umstellen und mit der Mitternachtsformel dann auf die krude Wurzel-Quadrat-Gleichung kommen.
Und für e1=e2 und e3=e1+e0 rd der interne Zins durch -e1/e0 ermittelt - das kann man sich ja doch ganz gut merken. 😉 Und ist auch logisch, denn nachschüssige Zinsen in kontanter Höhe und zusätzlich in der letzten Periode die Rückzahlung der Anfangsauszahlung ist ja nix anderes, als wenn ich 1000 Euro auf ein Sparbuch lege und die 0,36 Euro, die ich dafür aktuell an Zinsen bekomme, immer am Jahresende abhebe.
Naja... "einfach nach (1+r) auflösen", ist gut gesagt 😉. Wenn man's kann... Alles ist machbar, aber nicht 4 Tage vor Klausur! Man braucht Kenntnisse zur quadratischen Ergänzung und zur biquadratischen Gleichungen... die PQ-Formel miteinbegriffen...
Ich hatte bei keinem Teilgebiet so viel Bauchschmerzen wie heute beim internen Zinsfuss. Gut, ich habe ihn erst heute gelernt, weil ich davon ausging, dass wir ihn nicht brauchen. Vielleicht kommt der mir deswegen so unvertraut und unwirklich vor.
Ich hatte bei keinem Teilgebiet so viel Bauchschmerzen wie heute beim internen Zinsfuss. Gut, ich habe ihn erst heute gelernt, weil ich davon ausging, dass wir ihn nicht brauchen. Vielleicht kommt der mir deswegen so unvertraut und unwirklich vor.
Zuletzt bearbeitet:
Jup, du hast recht. Hatte mich vertanIch bin es schon wieder! Deine Skizze hat einen kleine Fehler:
Projekt A: K(r=0) = 456 -> zinsfuß = 10%
Projekt B: K(r=0) = 405 -> zinsfuß = 11,25%
A hat also den höheren y-Achsenabschnitt schneidet aber die x-Achse früher als B -> die Kurven müssen sich schneiden.
Schau mal nach, du hast die falschen Punkteverbunden.
Sorry für das Hochholen des alten Posts, aber das hier lässt mich schon länger nicht los:
Sonderfall 4 sagt:
Von daher gilt es doch dann die Gleichung zu lösen (geht dank der "einfachen" Zahlen sogar) - ist das Zufall und alle, die das so einfach gerechnet haben, hatten Glück?
Da der Rückfluss über die 3 konstant ist und und die Rückzahlung zum Nennwert erfolgt lässt sich der interne Zins ganz einfach ermitteln
135/1200 = 11,25 %
Sonderfall 4 sagt:
Seite 43 aus Investitionsentscheidungen schrieb:eine Investition, bei der auf eine einzige Auszahlung im Zeitpunkt t = 0 in allen zukünftigen Zeitpunkten t = 1, 2, …, T konstante Einzahlungen in Höhe von e folgen
Wieso darf das dann hier angewendet werden? Die Rückflüsse sind nicht konstant, da auch, wenn ich von den 1335 die 135 abziehe, immer noch 1200 übrig bleiben. Auch ist T mit 4 nicht wirklich hinreichend groß. Damit die Annäherung passt, muss T schon mind. 30, besser 50 Jahre sein..daß für hinlänglich große Laufzeiten T der Ausdruck
RBF (T, r*) durch 1/r* approximiert werden kann
Von daher gilt es doch dann die Gleichung zu lösen (geht dank der "einfachen" Zahlen sogar) - ist das Zufall und alle, die das so einfach gerechnet haben, hatten Glück?
Ich versuch mich ja nur an die Definition im Kurstext zu halten. Dein Beispiel kann ich nachvollziehen und verstehe auch dabei den Sinn der Rechnung. Ist dann aber nicht Sonderfall 4, sondern meinetwegen ein undokumentierter Sonderfall x (meinewegen auch "logisches Denken"), der (was) definitiv nicht im Kurstext steht - danke dafür, dann verwende ich das so, falls es eine Reihe so aussieht.
Mit der Zahlungsreihe (-1200, 135, 135, 1500) würde es also nicht funktionieren.
Mit der Zahlungsreihe (-1200, 135, 135, 1500) würde es also nicht funktionieren.
Eigentlich ist das nichts anderes als ein endfälliges Darlehen ohne Disagio, da gilt ja auch Nominalzins = Effektivzins.
Ich denke das soll der Witz an der Aufgabe sein, dass es gerade kein Sonderfall ist. Theoretisch kannst Du auch mit dieser Näherungsformel für den Effektivzins bei endfälligen Darlehen rechen, da kommst Du dann auch auf das Ergebnis.
Ich denke das soll der Witz an der Aufgabe sein, dass es gerade kein Sonderfall ist. Theoretisch kannst Du auch mit dieser Näherungsformel für den Effektivzins bei endfälligen Darlehen rechen, da kommst Du dann auch auf das Ergebnis.