Wagner/Within Verfahren - Beispiel KE2 Seite 41 ff.

Ramona,


Gibt es insgesamt 0 < m Perioden, so wird für jeden "Periodenhorizont" t = 1, 2, 3, ..., m (im KE Beispiel ist m = 6) die kostengünstigste Bestellpolitik bestimmt und zwar so:

Werden t <= m Perioden betrachtet dann werden für alle j = 1...t die Gesamtkosten Kj(t) berechnet die sich ergeben, wenn in Periode j alle Bedarfe der Perioden j, j + 1, ..., t mitbestellt werden - und zwar inklusive der Kosten für die Deckung der Bedarfe für die Perioden < j - diese Kosten wurden bis dahin schon berechnet, d.h. hier kommt die Rekursion ins Spiel.

Das Minimum K(t) = min{ K1(t), ... Kt(t) } gibt dann die kostengünstigste Bestellpolitik für t Perioden an.

Das ist der erste Schritt bei Wagner/Whitin ("Vorwärtsrekursion").

Daran schließt sich der zweite Schritt an ("Rückwärtsrekursion"), der die kostengünstigste Politik bei m Perioden bestimmt, bei der letzten Periode beginnend (im Beispiel Periode 6). Das ist nur ein "rückwärts verfolgen" des kostengünstigsten Bestell-Pfades (siehe Beitrag #6).

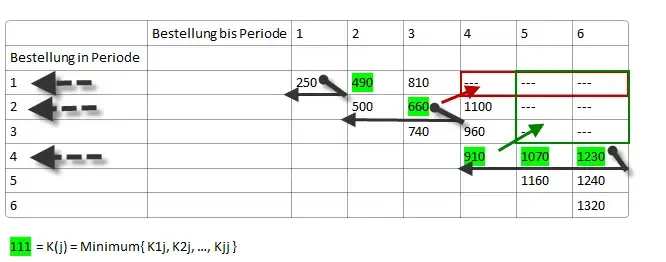
Beispiel (1. Schritt):

Für t = 4 Perioden sind also zu berechnen: K1(4), K2(4), K3(4), K4(4)

ra_mona schrieb:

durch welche Rechnung kommt man auf 1100?

Zum Vergrößern anklicken....

Es ist K2(4) = 1100 GE, denn:

K2(4) sind die Gesamtkosten, wenn der Bedarf der Perioden 2, 3, 4 in Periode 2 bestellt wird.

K2(4) enthält die Kosten, die bis dahin angefallen sind, d.h. die Kosten zur Deckung des Bedarfs in Periode 1. Das sind nur die bestellfixen Kosten 250 GE für die Bestellung in Periode 1.

K2(4) enthält ausserdem die bestellfixen Kosten für die Bestellung der Bedarfe der Perioden 2, 3, 4 in Periode 2, also weitere 250 GE.

K2(4) enthält ausserdem Lagerkosten:

Lagerkosten für den Bedarf x3 = 80 ME in Periode 3, der 3 - 2 = 1 Periode lagert: 1 * 80 ME * 2 GE/ME = 160 GE.

Lagerkosten für den Bedarf x4 = 110 ME in Periode 4, der 4 - 2 = 2 Perioden lagert: 2 * 110 ME * 2 GE/ME = 440 GE.

Damit ist K2(4) = 250 GE + 250 GE + 160 GE + 440 GE = 1100 GE

Liebe Grüße

ChrissiLLB schrieb:

Für die Planungsperiode 4 sind also zu berechnen: K1(4), K2(4), K3(4), K4(4)

Zum Vergrößern anklicken....

K1(4): Alle Bedarfe der Perioden 1 bis 4 werden in Periode 1 bestellt:

- Bestellfixe Kosten für die Bestellung in Periode 1: 250 GE

- Lagerkosten für x2 = 120 für 1 Periode: 1 * 120 * 2 = 240 GE

- Lagerkosten für x3 = 80 für 2 Perioden: 2 * 80 * 2 = 320 GE

- Lagerkosten für x4 = 110 für 3 Perioden: 3 * 110 * 2 = 660 GE

Also: K1(4) = 250 + 240 + 320 + 660 = 1470 GE

===========================================

K2(4): Alle Bedarfe der Perioden 2 bis 4 werden in Periode 2 bestellt:

Das habe ich oben berechnet: K2(4) = 1100 GE

===========================================

K3(4): Alle Bedarfe der Perioden 3 bis 4 werden in Periode 3 bestellt:

- Minimale Kosten für alle Bedarfe der Periode 1 bis 2: K(2) = 490 GE (siehe KE S. 42 unten).

- Bestellfixe Kosten für die Bestellung in Periode 3: 250 GE

- Lagerkosten für x4 = 110 für 1 Periode: 1 * 110 * 2 = 220 GE

Also: K3(4) = 490 + 250 + 220 = 960 GE

===========================================

K4(4): Alle Bedarfe der Perioden 4 bis 4 wird in Periode 4 bestellt:

- Minimale Kosten für alle Bedarfe der Periode 1 bis 3: K(3) = 660 GE (siehe KE S. 43 Mitte).

- Bestellfixe Kosten für die Bestellung in Periode 3: 250 GE

- Es fallen keine Lagerkosten an.

Also: K4(4) = 910 GE

Minimal ist K(4) = min{ K1(4), K2(4), K3(4), K4(4) } = min {1470, 1100, 960, 910 } = 910 = K4(4).

Es ist also für 4 Perioden am kostengünstigsten in Periode 4 eine neue Bestellung durchzuführen, die den Bedarf der Periode 4 deckt.

Liebe Grüße

ra_mona schrieb:

Bei Planungshorizont 5 und 6 verlassen sie mich dann ganz... 🙂

Zum Vergrößern anklicken....

5 Perioden: K(5) = min {K1(5), K2(5), K3(5), K4(5), K5(5) }

K1(5): Die Bedarfe der Perioden 1 bis 5 werden in Periode 1 bestellt:

K1(5)
=
250 GE
+ 1 * 120 * 2 GE
+ 2 * 80 * 2 GE
+ 3 * 110 * 2 GE
+ 4 * 80 * 2 GE
= 2110 GE

K2(5): Die Bedarfe der Perioden 2 bis 5 werden in Periode 2 bestellt:

K2(5)
=
250 GE (= K(1))
+ 250 GE
+ 1 * 80 * 2 GE
+ 2 * 110 * 2 GE
+ 3 * 80 * 2 GE
= 1580 GE

K3(5): Die Bedarfe der Perioden 3 bis 5 werden in Periode 3 bestellt:

K3(5)
=
490 GE (= K(2))
+ 250 GE
+ 1 * 110 * 2 GE
+ 2 * 80 * 2 GE
= 1500 GE

K4(5): Die Bedarfe der Perioden 4 bis 5 werden in Periode 4 bestellt:

K4(5)
=
660 GE (= K(3))
+ 250 GE
+ 1 * 80 * 2 GE
= 1070

K5(5): Die Bedarfe der Perioden 5 bis 5 werden in Periode 4 bestellt:

K5(5)
=
910 GE (= K(4))
+ 250 GE
= 1160 GE

Also: K(5) = min {K1(5), K2(5), K3(5), K4(5), K5(5) } = K4(5) = 1070

Es ist bei 5 Perioden also am kostengünstigsten in der Periode 4 für Periode 4 und 5 zu bestellen.

Liebe Grüße

ra_mona schrieb:

Bei Planungshorizont 5 und 6 verlassen sie mich dann ganz... 🙂

Zum Vergrößern anklicken....

6 Perioden: K(6) = min{ K1(6), ..., K6(6) }

K1(6): Es wird in Periode 1 für die Perioden 1 - 6 bestellt:

K1(6)
=
250 GE
+ 1 * 120 * 2 GE
+ 2 * 80 * 2 GE
+ 3 * 110 * 2 GE
+ 4 * 80 * 2 GE
+ 5 * 40 * 2 GE
= 2510 GE

K2(6): Es wird in Periode 2 für die Perioden 2 - 6 bestellt:

K2(6)
=
250 GE (= K(1))
+ 250 GE
+ 1 * 80 * 2 GE
+ 2 * 110 * 2 GE
+ 3 * 80 * 2 GE
+ 4 * 40 * 2 GE
= 1900 GE

K3(6): Es wird in Periode 3 für die Perioden 3 - 6 bestellt:

K3(6)
=
490 GE (= K(2))
+ 250 GE
+ 1 * 110 * 2 GE
+ 2 * 80 * 2 GE
+ 3 * 40 * 2 GE
= 1520 GE

K4(6): Es wird in Periode 4 für die Perioden 4 - 6 bestellt:

K4(6)
=
660 GE (= K(3))
+ 250 GE
+ 1 * 80 * 2 GE
+ 2 * 40 * 2 GE
= 1230 GE

K5(6): Es wird in Periode 5 für die Perioden 5 - 6 bestellt:

K5(6)
=
910 GE (= K(4))
+ 250 GE
+ 1 * 40 * 2 GE
= 1240 GE

K6(6): Es wird in Periode 6 für die Perioden 6 - 6 bestellt:

K6(6)
=
1070 GE (= K(5))
+ 250 GE
= 1320 GE

Damit: K(6) = min {K1(6), ..., K6(6) } = K4(6) = 1230 GE

Es ist also für 6 Perioden am kostengünstigsten in Periode 4 eine neue Bestellung durchzuführen, die den Bedarf der Periode 4, 5, 6 deckt.

Liebe Grüße

ChrissiLLB schrieb:

Daran schließt sich der zweite Schritt an ("Rückwärtsrekursion"), der die kostengünstigste Politik bei m Perioden bestimmt.

Zum Vergrößern anklicken....

Jetzt wird von hinten nach vorne "abgehakt".


Bisher wurde berechnet:

K(1) = K1(1) = 250 GE

K(2) = K1(2) = 490 GE

K(3) = K2(3) = 660 GE

K(4) = K4(4) = 910 GE

K(5) = K4(5) = 1070 GE

K(6) = K4(6) = 1230 GE

Von hinten beginnend:

K(6) = K4(6), d.h. in Periode 4 wird für Periode 4, 5, 6 bestellt: p46

Damit sind die Perioden 4, 5, 6 abgehakt.

K(3) = K2(3), d.h. in Periode 3 wird für Periode 2 und 3 bestellt: p23

Damit sind die Perioden 2, 3 angehakt.

K(1) = K1(1), d.h. in Periode 1 wird für Periode 1 bestellt: p11

Die kostengünstigste Bestellpolitik ist also (p11, p23, p46).

Gesamtkosten: K = K(6) = K4(6) = 1230 GE

Liebe Grüße

Wow, vielen Dank!!! Hatte mich heute auch damit beschäftigt und kam auch nicht weiter. Werde ich nachher gleich mal durcharbeiten.

vielen lieben Dank 🙂)
super! Habe deine Beiträge erst gerade gesehen...werde mir heute abend alles in Ruhe mal anschauen.
Danke!
LG ra_mona

Ich habe oben das Entscheidungshorizont-Theorem nicht beachtet und deshalb unnötig viele Werte berechnet. Hier die Lösung in Tabellendarstellung. Tabelleneinträge ohne Kosten (die mit "---") sind genau die, die wegen des Entscheidungshorizont-Theorem nicht berücksichtigt/berechnet werden müssen (weil sie sicher zu höheren Kosten führen).




Liebe Grüße

ich weiß, dass der Thread schon alt ist. Aber kann mir bitte jemand erklären wie mann zu 660GE, 910GE und 1070GE kommt. Bzw. kann mir wer helfen, dieses ähnliches Beispiel zu lösen?
Period= 1, 2, 3, 4, 5, 6
Bedarf= 75, 5, 33, 28, 15, 10
Rüstkosten beträgt 80GE
Lagerkosten ist 2GE. Wagner/Whitin verfahren verwenden und kostengünstigten Bestellpolitik ermitteln!